T31

Chapitre 3  Economie Publique

Partie 1 : Préférences individuelles et choix collectif

1. Introduction

L’objet essentiel de « l’économie » est la gestion des ressources. La science économique étudie de façon descriptive (ou « positive ») mais aussi de façon normative les procédures qui conduisent à la répartition des ressources entre les membres d’une société. D’un point de vue théorique, une des premières missions de l’économie est de mettre en évidence les procédures d’allocation ou de répartition « optimales » : existe-t-il des procédures plus désirables que d’autres pour distribuer (et produire) des biens? Comment sont elles définies? Peut on déduire de cette étude des recommandations opérationnelles en termes d’organisation économique?

L’objectif de ce chapitre est l’étude du problème de base de l’économie : peut on, à partir de préférences individuelles nécessairement conflictuelles, aboutir à des choix collectifs rationnels.

Données du problème :

On suppose qu’il existe un ensemble A de décisions collectives. L’ensemble A représente ainsi l’ensemble des options sur lequel la société doit décider. A pourra par exemple représenter l’ensemble des différentes façons de distribuer des ressources aux membres d’une société. Chaque individu de la société a bien sûr une idée du meilleur choix pour lui parmi toutes les options de l’ensemble A. Il n’y a aucune raison a priori d’obtenir un consensus. Autrement dit, les individus n’ont pas tous les mêmes préférences sur A.

Le problème consiste donc à savoir quelles sont les « meilleures » procédures qui permettent de passer de préférences individuelles (a priori contradictoires) à une décision collective rationnelle. Ce problème est totalement similaire à celui que l’on rencontre lorsqu’on a à comparer des options et que l’on dispose de plusieurs critères de comparaison. Il existe, dans la vie de tous les jours, de nombreux exemples ou ce type de problème se pose . En compétition automobile on doit décerner le titre de champion (décision) au vu des résultats sur les différentes courses (critères individuels) de l’année. Ici les « individus » sont les courses : chaque course permet de classer sans ambiguïté les différents concurrents; c’est à dire, dans le langage de l’économie, met en évidence une « préférence » parmi les coureurs. Le mécanisme qui permet d’attribuer le titre doit tenir compte de tous les résultats de manière la plus rationnelle possible. De même, le classement des candidats à un concours doit refléter leurs performances sur un certain nombre de disciplines différentes. Enfin, la décision du tracé d’une autoroute dépend a priori de différents critères comme le coût, l’impact sur l’environnement, le temps gagné, le décongestionnement des autres itinéraires...

2. Préférences individuelles

Définition : Préférence individuelle

une préférence individuelle notée (on dit « préféré ou indifférent à »), ou critère, sur un ensemble A d’options possibles est une relation totale, réflexive et transitive (ce type de relation est appelé pré-ordre total) :

relation totale : , on peut toujours comparer deux options de A

réflexive :, une option est toujours préférée ou indifférente à elle-même (évidemment indifférente!).

transitive : , si a est préférée à b et b à c alors a est préférée à c.

La transitivité traduit une condition minimale de rationalité : on imagine mal qu’un individu puisse dire, toutes choses égales par ailleurs, qu’il préfère c à a alors qu’il déclare préférer a à une troisième option meilleure que c pour lui!

Il faut noter qu’un pré-ordre est moins exigeant qu’un ordre au sens ou il tolère l’indifférence entre options différentes : pour une relation d’ordre (par exemple « plus grand que » dans l’ensemble des nombres) indifférence signifie égalité.

Définition : Préférence stricte

étant donné un préordre ,

on dit que a est strictement préféré à b que l’on note , si et seulement si :

on dit que a est indifférent à b que l’on note , si et seulement si :

Il est commode de représenter une relation par son diagramme. Il y a une flèche de a vers b lorsque et un trait simple lorsque

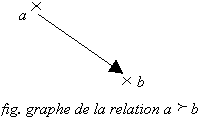
Sur le graphe, la transitivité se traduit par l’absence de cycle dans la relation (cf fig.)

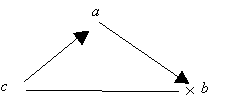
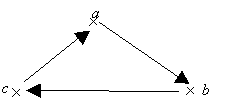
fig. exemple de relations non transitives

3. Procédure de choix collectif

Supposons maintenant qu’il y ait n individus ayant chacun une préférence . Le problème qui se pose est alors de définir une procédure qui agrège ces préférences individuelles en une préférence collective. Autrement dit, on voudrait définir un mécanisme qui donne un préordre unique fonction de l’ensemble des préférences individuelles.

Définition : Profil

On appelle «  profil » un n-uplet de préférences individuelles :. Un profil correspond à un état particulier des préférences individuelles.

Pour prendre une image, un profil correspond à « un état de l’opinion » concernant les éléments de A. On conçoit alors que lorsque le profil varie, l’opinion collective doit varier aussi. Le problème est de savoir comment cette préférence collective doit varier.

On voudrait donc définir une procédure qui permette d’associer à chaque profil possible un préordre « collectif » unique. Si l’on reprend les exemples précédents cela revient à définir la règle qui permet d’établir un classement annuel des pilotes en fonction des résultats des différentes courses de l’année. De la même façon, cela consiste à définir le règlement du concours qui donne la procédure de prise en compte des notes dans les différentes matières pour établir le classement final.

Définition : Agrégation

on appelle procédure d’agrégation de préférence (ou fonctionnelle de choix social...) une application de l’ensemble des profils vers l’ensemble des préordres su A :

préordre sur A.

Quelles propriétés doit satisfaire cette application? On conçoit aisément que toutes les manières d’agréger n’ont pas les bonnes propriétés : il serait par exemple curieux de définir un procédure qui décerne le titre de champion à un pilote arrivé dernier à toutes les courses! On sent ainsi que parmi l’ensemble des procédures d’agrégation, certaines doivent être écarter parce qu’elles sont manifestement irrationnelles. Mais alors, quelles sont les propriétés de rationalité que l’on aimerait avoir?

3. Propriétés minimales de rationalité

Le premier principe évident est le principe d’unanimité : si tous les critères ou individus classent l’option a avant l’option b alors le classement agrégé doit respecter cette hiérarchie :

Définition : unanimité (Pareto)

Propriété d’unanimité (stricte) : on dit que vérifie la propriété d’unanimité stricte si :

La seconde propriété est appelée propriété d’indépendance : elle dit que le classement collectif entre deux options ne doit dépendre que de la configuration des préférences individuelles sur ces deux options. Autrement dit si pour deux profils différents (par exemple deux saisons consécutives de formule 1), deux options a et b ont exactement les mêmes positions relatives pour les différents critères (a est arrivé devant b (et réciproquement ) dans les mêmes courses d’une année sur l’autre), alors le classement collectif entre a et b doit rester inchangé.

Définition : Indépendance

Propriété d’indépendance (Arrow)

vérifie la propriété d’indépendance si :

deux profils, si deux options a et b sont telles que alors :

Pour bien comprendre ce que signifie cette propriété il est intéressant de donner des exemples de procédures qui ne la vérifient pas!

Exemples

Un dessert pour trois

Trois convives terminent un repas au restaurant. Ayant bien dîné ils décident de partager le dessert en trois. Ils appellent le serveur et lui demandent ce qu’il propose. Celui-ci répond qu’ils ont le choix entre glace (G), pâtisserie (P) ou fruits (F). Comme ces trois convives ont un grand souci de démocratie, ils décident d’utiliser une procédure d’agrégation de préférence. Celle-ci détermine que la glace (G) doit être le meilleur choix collectif. Avant même de prendre leur commande le serveur revient désolé en leur disant qu’il vient d’apprendre qu’il n’y a plus de fruits. Par acquis de conscience, les trois compères recalculent et trouvent curieusement que le dessert qu’ils doivent commander n’est plus la glace mais la pâtisserie (P). Ce type de revirement apparaît totalement irrationnel au sens ou un individu seul n’aurait jamais eu ce type de comportement. Pourtant, un certain nombre de procédures d’agrégation de préférences ou de critères ont ce type de défauts. L’exemple le plus simple est la procédure de type « championnat » de formule 1 appelée règle de Borda.

Règle de Borda

La règle de Borda permet d’établir un classement à partir des résultats sur plusieurs « courses » ou critères de la manière suivante. Prenons l’exemple de trois courses et quatre coureurs. A chaque course le vainqueur est crédité de 4 points, le second de 3 points le troisième de 2 point et le dernier de 1. En additionnant les points obtenus par chaque joueur on obtient un classement général. Prenons l’exemple suivant :

Course 1 : A>B>C>D soit : 4 points pour A, 3 pour B, 2 pour C et 1 pour D.

Course 2 : D>A>B>C soit : 3 points pour A, 2 pour B, 1 pour C et 4 pour D.

Course 3 : C>A>B>D soit : 3 points pour A, 2 pour B, 4 pour C et 1 pour D.

Course 4 : C>A>B>D soit : 3 points pour A, 2 pour B, 4 pour C et 1 pour D.

course 5 : C>A>D>B soit : 3 points pour A, 1 pour B, 4 pour C et 2 pour D

Ce qui donne : 16 points pour A, 10 pour B, 15 pour C et 9 pour D. A est donc déclaré champion devant C. Cependant, supposons que l’on découvre que la voiture de B n’est pas conforme au règlement et, qu’en conséquence on décide de déclasser B dans toutes les courses. On obtient alors le résultat suivant :

Course 1 : A>C>D>B soit : 4 points pour A, 1 pour B, 3 pour C et 2 pour D.

Course 2 : D>A>C>B soit : 3 points pour A, 1 pour B, 2 pour C et 4 pour D.

Course 3 : C>A>D>B soit : 3 points pour A, 1 pour B, 4 pour C et 2 pour D.

Course 4 : C>A>D>B soit : 3 points pour A, 1 pour B, 4 pour C et 2 pour D.

course 5 : C>A>D>B soit : 3 points pour A, 1 pour B, 4 pour C et 2 pour D

Ce qui donne alors toujours 16 points pour A, mais 17 pour C qui devient champion de ce fait!

On voit dans cet exemple que le classement entre A et C dépend des performances d’un troisième conducteur.

Exercice : cliquer ici

Définition : Procédures « dictatoriales »

on dit que la procédure est dictatoriale lorsqu’il existe un individu i (ou un critère) tel que pour tout couple (a,b) dans AXA, . Autrement dit, dans une procédure dictatoriale, un individu impose ses préférences strictes.

Théorème d’Arrow

Si le nombre de décisions est supérieur à 3,les seules procédures qui permettent d’agréger n’importe quel profil en une préférence collective qui vérifient le principe d’unanimité stricte et le principe d’indépendance sont les procédures dictatoriales.

Ce résultat peut apparaître comme un résultat extrêmement négatif. Il dit en gros que la démocratie est impossible puisque les seules procédures « raisonnables » au sens des deux propriétés requises sont les procédures où les choix critiques sont laissés à un seul individu. Il faut voir cependant que ce que l’on exige est ici très fort. D’une part on demande que la procédure prévoit un résultat pour tous les profils de préférences envisageables. On peut penser au contraire que même s’il différent, les préférences des individus ne sont pas quelconques c’est à dire varient sans décrire totalement l’ensemble de tous les préordres sur A. On montre qu’en relâchant la contrainte dite de domaine universel, c’est à dire en contraignant la variabilité des préférences, on peut définir des procédures rationnelles (exercices : cliquer ici).