T34

Chapitre 3 : Economie Publique

Partie 4 : Modèles de Taxation

1. Le deuxième théorème

Une dichotomie entre efficacité et équité

Le deuxième théorème de l’économie normative nous apprend que l’on peut obtenir n’importe quelle allocation efficace au sens de Pareto, autrement dit n’importe quelle allocation sans gaspillage, comme résultat d’un équilibre concurrentiel à condition d’opérer, ex ante, une redistribution adéquate des ressources initiales. Selon ce théorème, il n’existe pas intrinsèquement d’incompatibilité entre des objectifs d’efficacité et des objectifs d’équité ou de redistribution : si, pour une raison ou une autre, la collectivité n’est pas satisfaite du résultat de l’équilibre concurrentiel, si elle trouve par exemple qu’il y a trop d’inégalité de niveaux de vie, alors une simple redistribution des ressources initiales permet de redresser les choses tout en étant certain que cette procédure n’affectera pas l’efficacité du système. On peut illustrer très simplement ce théorème à l’aide d’une boîte d’Edgeworth avec deux biens [1] et [2] et deux consommateurs A et B. Chaque agent dispose de dotation initiales en biens 1 et 2 : et échange sur un marché selon un processus concurrentiel. On raconte alors la petite histoire suivante : pendant la semaine chaque agent produit son panier de ressources initiale en travaillant par exemple dans ses champs. Le dimanche, tous les agents se retrouvent sur la place du village et échangent leurs productions. Si l’on pose , une allocation réalisable des ressources vérifiera . Un allocation réalisable est représentée par un point dans le rectangle de cotés w₁, w₂ .

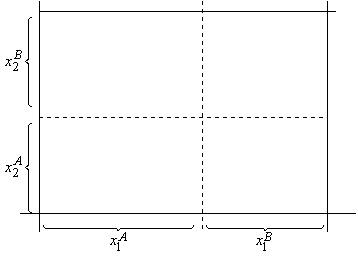
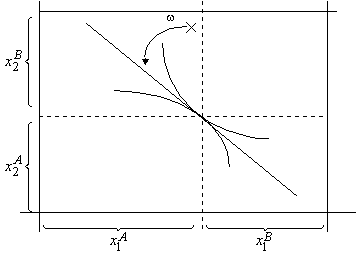
Dans ces conditions une allocation efficace est un point de la boîte d’Edgeworth où les deux courbes d’indifférence des deux agents sont tangentes. Ce point est obtenu comme équilibre concurrentiel pour peu que l’allocation initiale soit sur la (une) droite tangente commune aux deux courbes d’indifférence. Le deuxième théorème dit simplement que si les ressources initiales ne sont pas sur cette droite il suffit que l’Etat redistribue (flèche courbe sur le graphique) de manière à faire en sorte que la “ nouvelle ” allocation initiale soit sur cette droite.

Ce deuxième théorème a une vertu essentielle : Il dit que la redistribution initiale n’a pas besoin de se soucier d’efficacité, c’est le marché qui, une fois la redistribution initiale faite, ajustera l’allocation de manière efficace. Pourquoi y-a-t-il cette dichotomie entre efficacité et redistribution? Tout simplement parce que nous avons une hypothèse sous-jacente selon laquelle la redistribution des ressources initiales n’affecte pas “ la production ” de ces ressources initiales par les agents.

Un problème d’information

Si l’on suppose, avec un peu plus de réalisme, que la production des ressources initiales correspond à un processus volontaire de chacun des agents, alors la politique de redistribution a une incidence sur les comportements. L’étendue de cette modification de comportement dépend crucialement de l’information dont dispose l’Etat et, par la même, de la forme de l’instrument fiscal de redistribution. Précisons ce point.

Tout d’abord, pour tenir compte de la rétroaction de la politique de redistribution sur “ la production ”, il faut rajouter un bien (par exemple le travail ou l’effort) dans le modèle ci-dessus, et incorporer l’arbitrage individuel entre travail et consommation. Dans ces conditions, examinons l’incidence d’une politique de redistribution sur le comportement des agents. Plaçons nous, par exemple, dans le cas de la boîte d’Edgeworth ci-dessus. Sans taxation on voit que A est plus productif que B (au moins en bien 2). De deux choses l’une,

ou bien l’Etat sait que A est plus productif et a les moyens de le prouver,

ou bien l’Etat ne peut qu’observer les ressources initiales et ne peut donc mettre en place qu’une formule de taxation fonction explicite du revenu.

Dans le premier cas l’Etat peut imposer (!) une redistribution nominative. Schématiquement l’Etat pourra dire : “ je sais que A est plus productif, je prélève donc une quantié forfaitaire (indépendante de son vrai revenu) sur son panier initial, quantité que je redistribue à B ”. Dans ces conditions A va modifier son comportement de production mais cette modification n’est pas, en fait, préjudiciable à l’efficacité : il va simplement ajuster son travail en fonction de son arbitrage individuel entre loisir et consommation. En particulier il est tout a fait vraisemblable que A ait intérêt à augmenter son activité de production pour compenser le prélèvement qu’il doit subir. Dans ce cas l’impôt (forfaitaire) est plutôt incitatif, au sens où il induit les agent à augmenter leur activité productrice. Il s’agit de la traduction du classique effet de revenu de la micro-économie.

Dans le second cas, lorsque l’Etat n’observe que le revenu, il n’est plus possible de proposer un impôt nominatif. La seule possibilité consiste à afficher un barême qui donne le montant de l’impôt (positif ou négatif) en fonction du revenu initial. L’Etat ne peut plus dire : “ je sais que A est plus productif donc je peux lui prélever une partie de son revenu ”, il peut seulement affirmer “ je prélèverai au plus riche pour donner au plus pauvre ” et cette nuance est cruciale. En effet l’arbitrage de A n’est plus du tout le même que précédemment. La question essentielle pour A est de savoir si l’effort de production incrémental entre un faible revenu et un fort revenu avant impôt est correctement rémunéré compte tenu du barême de redistribution. Un autre façon, plus caricaturale, de décrire cet arbitrage consiste dire que la question pour A est de savoir s’il ne vaut mieux pas “ être pauvre ” et bénéficier des subventions plutôt que “ d’être riche ” et se faire taxer. L’impôt a ici un effet clairement désincitatif (qui correspond au traditionnel effet de substitution de la micro-économie) et l’on pressent que le résultat sera inefficace au sens de Pareto dans l’économie à trois bien. Dans ce second cas de figure il n’y a donc plus de dichotomie entre l’objectif d’efficacité et celui d’équité.

2. Un modèle simple à deux biens

Dans ce modèle, nous supposons qu’il n’y a pas du tout d’effet de revenu. Une taxation nominative forfaitaire ne modifie pas le comportement d’offre de travail de la part des agents. Ici, tous les agents sont identiques et arbitrent entre consommation et travail selon la fonction d’utilité où v est une fonction croissante convexe. Les agents different par leur productivité w. Autrement dit, un agent de type w obtient un revenu brut R=wL s’il travaille L. Le revenu brut d’un individu de type w auquel on prélève une taxe forfaitaire T ne dépend pas de T. est en effet solution de :

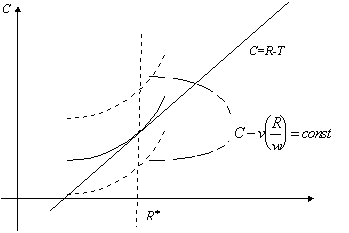
Supposons par exemple qu’il y a deux types d’agents avec w₁<w₂. Soient T₁ et T₂ le montant des taxes forfaitaires que l’Etat impose sur chacun des deux agents. Compte tenu de la convexité de v on a nécessairement . Sur la graphique suivant on a représenté la situation pour deux valeurs particulières de T₁ et T₂.

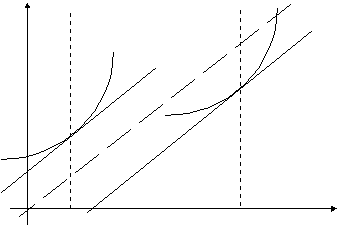
Du fait de l’absence d’effet de revenu, on a ici un résultat particulièrement simple. En fonction de la taxe T_i , l’allocation finale se déplace, pour chacun des agents, sur la droite verticale . Si par exemple, à budget constant, on veut augmenter la taxe sur le plus productif au profit du moins productif (redistribution dans un sens “ normal ”) on déplace l’allocation de 2 vers le bas tandis qu’on fait monter l’allocation de 1. Jusque là la redistribution n’est en rien préjudiciable à l’efficacité puisque le revenu brut total reste inchangé. L’allocation qui en résulte est Pareto efficace.

On peut se poser alors la question de savoir si une telle allocation peut être obtenue lorsque l’information est incomplète, c’est à dire lorsque l’Etat est dans l’incapacité d’observer la productivité individuelle. Une solution évidente consiste alors à proposer (au lieu d’une taxation forfaitaire) un barême d’impôt qui donne le montant prélevé en fonction du revenu observé. Peut-on obtenir l’allocation précédente (efficace) à l’aide d’un barème d’impôt bien calculé?

Prenons l’allocation correspondant aux taxes forfaitaires T1 et T2. Supposons que cette allocation puisse être obtenue par l’Etat au moyen d’un barème d’impôt du type . Cela impose en particulier que et que chaque agent, devant le barème d’impôt, choisisse un offre de travail compatible avec :

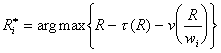
Ce ci impose en particulier que 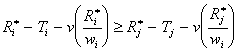que l’on peut réécrire pour i=2 et j=1:

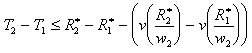
que l’on peut écrire aussi :

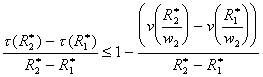
Pour que l’allocation efficace puisse être obtenue par un barème d’imposition il faut donc en particulier que le taux “ incrémental ” (membre de gauche de l’inégalité ci-dessus) attaché à la variation de revenu ne soit pas trop grand. C’est l’effet de substitution évoqué plus haut : la redistribution est limitée par l’effet désincitatif du barème d’impôt. On peut visualiser facilement cet effet désincitatif. Supposons que l’on veuille opérer une forte redistribution entre 1 et 2. Les allocation désirées sont représentées sur le graphique suivant. On voit alors que le taux incrémental d’imposition est trop grand : l’individu de type 2 préfère l’allocation () à l’allocation (), le surcroît d’effort de production n’est pas compensé par l’augmentation du revenu net.

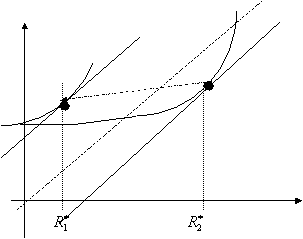
Ce modèle simple contient tous les ingrédients essentiels pour mettre en évidence l’aspect désincitatif associé à un barème d’impôt : en liant fonctionnellement montant prélevé et revenu observé, un barème d’impôt introduit une distorsion dans l’arbitrage “ loisir-consommation ”. Devant un barème d’impôt de type , un individu de type w choisira une offre de travail qui lui permette d’obtenir un revenu brut vérifiant :

C’est à dire solution de :

Alors que devant un impôt forfaitaire, le même individu choisira le revenu qui vérifie :

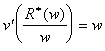
Du fait de la convexité de v on a bien sûr : .

C’est cet effet qui rompt la dichotomie entre redistribution et efficacité. C’est ce même effet qui fait dire que “ l’impôt tue l’impôt ”.

3. Un modèle continu

L’effet désincitatif limite d’une certaine manière les marges de manœuvre en terme de redistribution. Cet effet introduit la nécessité d’un arbitrage entre efficacité et amplitude de redistribution. Un modèle continu permet de mettre en évidence les principaux enjeux liés à cet arbitrage. On prend ici un modèle légèrement différent de celui présenté dans la section précédente : l’utilité d’un individu de type w pour un revenu R et une consommation C s’écrit : . Pour obtenir le revenu R, un individu de type w, doit développer un effort coûteux qui est équivalent à une diminution de consommation , avec , , . On suppose par ailleurs que w est distribué sur le segment avec une densité f(.), de cumulative F(.). L’objectif redistributif de l’Etat est résumé par une fonction de bien-être collectif qui est défini par une fonction U concave de sorte que :

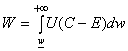
Supposons que l’Etat fixe un barème d’impôt sur le revenu de la forme . Chaque consommateur de type w ajuste alors son revenu de manière à maximiser son utilité :

Soit alors T(w) le niveau de taxe correspondant : .

Notons le revenu “ net-net ” de l’individu de type w : .

Par le théorème de l’enveloppe, (voir annexe) on a :

Le produit fiscal s’exprime alors de la manière suivante :

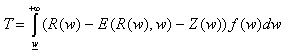
Le Bien-être collectif est égal à :

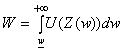
Le programme d’optimisation s’écrit alors, en notant l le coût d’opportunité des fonds publics :

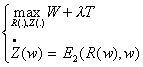
Une application directe des équations d’Euler Lagrange donne les conditions suivantes :

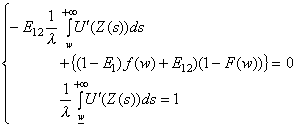
Posons :

On peut interpréter comme la valeur sociale marginale d’une unité de revenu distribué aux individu de productivité inférieure à w.

Les conditions d’optimalité s’écrivent alors :

Cette équation mérite un commentaire. Rappelons tout d’abord que la condition du premier ordre du programme maximisation du consommateur s’écrit :

Ainsi le membre de gauche de l’égalité est égal à , c’est à dire le montant d’impôt supplémentaire lorsque le revenu net augmente de 1. Ce ratio mesure en quelque sorte le taux marginal “ net ” d’imposition : taux marginal d’impôt par rapport au revenu net.

Le second membre de l’équation peut se décomposer en trois termes distincts.

peut aussi s’écrire : qui mesure l’élasticité de l’effort marginal par rapport à la productivité. Si cette élasticité est faible, cela signifie que l’effort marginal pour augmenter son revenu varie peu avec w. On peut relier cette élasticité à l’offre de travail lorsque E s’écrit . Dans ce cas l’offre de travail (sans impôt) est égale à , et son élasticité à w est égale à . On vérifie aisément qu’alors : . Ainsi, plus l’élasticité de l’offre de travail est grande plus le taux marginal d’imposition doit être petit. Le taux marginal d’imposition doit être diminué pour les sous-groupes de population pour lesquels on pense que la taxe est une forte incitation à la réduction de l’offre de travail.

Le second terme est l’inverse de ce que l’on appelle le taux de risque de la distribution des productivités. Le taux marginal d’imposition pour un revenu donné, doit être d’autant plus élevé qu’il y a une grande proportion d’individus ayant un revenu plus grand et au contraire très peu d’individus ayant ce revenu précis. Cet effet est parfaitement compréhensible de la manière suivante :objectif de redistribution mis à part, une augmentation du taux marginal d’imposition sur un tranche intermédiaire de revenu augmente mécaniquement les recettes fiscales sur les revenus plus élevés mais, par effet désincitatif, les diminue sur les revenus de la tranche concernée.

Le troisième terme résume le motif de redistribution. Dire que est plus grand que F signifie simplement que le poids “ social ” des individus ayant une faible productivité est plus grand que leur poids réel dans la population. Ainsi, plus la volonté de redistribution est forte ( élevé) plus le taux marginal d’imposition doit être fort (toutes autres choses égales par ailleurs).

Cette formule nous permet de discuter de certains points sur la progressivité de l’impôt. L’impôt sera dit progressif lorsque le taux marginal d’imposition est croissant avec le revenu. Le troisième terme (redistributif) peut se réécrire : , c’est à dire 1 moins la moyenne des utilités marginales sociales du revenu pour l’ensemble des individus ayant une productivité supérieure à w. Ce terme est croissant lorsqu’il y a une forte volonté redistributive : l’utilité marginale sociale du revenu est décroissante avec la productivité. Ce terme plaide, dans les cas normaux de volonté redistributive des riches vers les pauvres, pour une progressivité de l’impôt.

Le second terme est plus problématique. Pour une distribution (par exemple uniforme) sur un intervalle ce terme est très souvent décroissant et égal à zéro pour la productivité limite supérieure. Un taux marginal d’imposition nul pour les haut revenus est un résultat qui s’interprète typiquement en termes d’incitations et correspond au résultat que nous avons mis en évidence dans le cas de deux agents. Notons qu’un impôt dégressif n’est pas contradictoire avec une volonté redistributive des hauts revenus vers les bas revenus. Par exemple le barème d’impôt peut comporter une composante négative fixe (revenu fixe redistribué à tout le monde) et une composante marginale décroissante : , avec j’ décroissant. Pour des distributions infinies, tous les cas peuvent se présenter, on a pas nécessairement monotonie du taux de risque et l’analyse doit se faire au cas par cas. Le tableau suivant donne les valeurs des taux marginaux d’imposition optimaux pour une distribution lognormale de w et différents objectifs de redistribution. Il faut noter dans ce cas que la distribution lognormale (1-F)/wf décroit et tend vers zéro à l’infini. On parle d’objectif Rawlsien lorsque seul le poids des plus défavorisés est pris en compte dans la fonction objectif (ici les 15% les plus pauvres), et d’objectif de type “ Gini ” lorsque le ” poids de chaque individu décroît comme 1-F. L’élasticité de l’offre de travail est prise égale à 0,3.

Percentiles de la distribution de w	Objectif Rawlsien	Objectif de type “ Gini ”
Médiane	84,4%	73%
quartile supérieur	77,4%	71,9%
décile supérieur	71,2	66,7
95%	67,2%	66,7
centile supérieur	62%	61,7%
99,9%	56,3%	56,2