T32
Chapitre 3 : Economie Publique
Partie 2 : Biens Publics
1. Introduction
Il
n’est pas rare, au cours d’une promenade à travers les villes ou dans certains
immeubles de faire l’expérience “ sensible ” des problèmes économiques
liés aux biens publics. Dans certains cas on constate facilement une différence
notable d’entretien, de propreté ou de modernité entre les espaces publics
(pelouses, allées, hall d’entrée d’immeuble, ...) et les locaux ou appartements
privés de la même rue ou du même immeuble.
Vous
pouvez même, en fonction de l’étendue de la différence, en deux mots en
fonction du contraste entre l’apparence des parties communes et le degré de
“ luxe ” des espaces privés, avoir une intuition du degré de l’
“ autorité ” et du “ pouvoir ” des instances collectives
chargées de la gestion des services communs.
On
sent bien intuitivement que la fourniture de ce type de bien et de service se
heurte à des problèmes spécifiques de décision et de financement qui conduisent
selon le mode de fonctionnement aux différences citées précédemment. D’où vient
le problème ?
En
simplifiant on peut dire que la difficulté vient de ce que le coût de mise en
place et aussi de fonctionnement de ce type de bien est difficilement “ individualisable ”
de manière “ rationnelle ” : lorsqu’un individu consomme ou
plutôt utilise (ou profite) de ce genre de service il ne le
“ détruit ” pas à due proportion, il engendre vraisemblablement un
coût marginal dû à l’usage mais ne consomme pas, au sens propre du terme le
bien en question. Pour forcer le trait, on peut imaginer des biens ou des
services dont le coût de production est complètement indépendant de la
fréquentation ou de l’usage. Lorsqu’on est en présence d’un bien privé tel que
la règle de la tarification au coût marginal suffise pour couvrir l’intégralité
des coûts, le problème évoqué ci-dessus ne se pose pas : financement et
décision efficace peuvent être atteints par le même instrument tarifaire.
L’efficacité est facilement “ décentralisable ” c’est-à-dire laissée
à la responsabilité do consommateur : si celui-ci veut consommer une unité
de plus, il sait que sa décision engendre un coût égal justement au coût
marginal, c’est-à-dire exactement égal au surcoût qu’il engendre. Dans notre problème
on ne dispose pas de cette règle simple. Si je me mets à la place du
fournisseur de service je pose alors le problème de la façon suivante :
supposons que je veuille mettre en place un service collectif dont je connais
le coût et que celui-ci est indépendant de la fréquentation. La première
question que je me pose est de savoir si le jeu en vaut la chandelle,
c’est-à-dire sir le coût est plus petit que les avantages retirés par les
consommateurs. Chaque utilisateur retire une certaine augmentation de bien-être
de ce service, c’est-à-dire qu’il est prêt à payer une certaine somme pour
jouir du service. Si en faisant la somme de ces consentements à payer et que
cette somme est supérieure au coût, je suis sûr que mon projet est intéressant.
Seulement le problème du financement n’est pas résolu pour autant :
comment faire pour “ forcer ” chaque individu à payer une somme égale
à son consentement à payer ; et ensuite comment répartir le surplus ?
2.
Exemple
Supposons
que je veuille construire une ligne de métro entre le centre-ville et
l’aéroport d’une grande ville de province. Je peux évaluer les coûts
d’investissement (génie-civil, voies, ouvrage d’art, tunnels divers et gares)
et les coûts de fonctionnement d’une telle ligne. Parmi tous ces coûts, certains
seront indépendants du trafic, d’autres seront variables avec la fréquentation
de la ligne.
On
supposera que l’ensemble des coûts fixes a une somme égale à ![]() (par an, par exemple)
et que le coût variable vaut m par voyageur × kilomètre. Le voyage est
un bien privé comme les autres : quand j’occupe une place dans le train je
la consomme au sens ou j’empêche un autre voyageur de voyager à cette place, en
revanche l’existence de la ligne et la fréquence des trains sont des services
collectifs au sens du paragraphe précédent.
(par an, par exemple)
et que le coût variable vaut m par voyageur × kilomètre. Le voyage est
un bien privé comme les autres : quand j’occupe une place dans le train je
la consomme au sens ou j’empêche un autre voyageur de voyager à cette place, en
revanche l’existence de la ligne et la fréquence des trains sont des services
collectifs au sens du paragraphe précédent.
Je
peux me poser le problème de savoir si une telle ligne est
“ collectivement ” intéressante. Pour cela, il faudrait que j’évalue
le consentement à payer (en sus de m) de chaque voyageur potentiel par
voyage, que j’en fasse la somme sur une année et que je la compare à ![]() . Par exemple, si l’on suppose qu’un consommateur
. Par exemple, si l’on suppose qu’un consommateur ![]() a un consentement à payer l’ensemble de ses voyages
a un consentement à payer l’ensemble de ses voyages ![]() (c’est par exemple,
au minimum, l’ensemble des coûts monétaires et non monétaires, nets des
avantages, associés à d’autres moyens de transports),
(c’est par exemple,
au minimum, l’ensemble des coûts monétaires et non monétaires, nets des
avantages, associés à d’autres moyens de transports), ![]() représente, d’une
certaines manière son consentement à payer la “ possibilité ” de
voyager en métro.
représente, d’une
certaines manière son consentement à payer la “ possibilité ” de
voyager en métro.
Dans
ces conditions, pour savoir si l’équipement vaut le coup, il suffit de comparer
:
(sur 1 an) ![]() et C.
et C.![]()
Même
si ![]() est supérieur à C,
on n’est pas sûr que la solution étudiée soit la meilleure.
est supérieur à C,
on n’est pas sûr que la solution étudiée soit la meilleure.
La procédure qu’il faut suivre consiste alors
à examiner des variantes pour voir si l’on ne peut pas augmenter la différence
entre la somme des consentements à payer et le coût. La meilleure solution sera
alors caractérisée par le fait que “ toute variante ” détériore la
différence entre ![]() et C.
Mathématiquement, cela signifie que la meilleure solution maximise
et C.
Mathématiquement, cela signifie que la meilleure solution maximise ![]() .
.
En supposant que les variantes peuvent être
définies de manière continue autour de la solution, cela signifie : en
notant ![]() et
et ![]() les variations
infinitésimales des grandeurs pertinentes, que l’on a, à l’optimum :
les variations
infinitésimales des grandeurs pertinentes, que l’on a, à l’optimum :
![]()
cette
condition (nécessaire) se lit : la somme des consentements marginaux à payer
pour une modification marginale du projet est égale au coût de cette
modification (coût supplémentaire entraîné par la modification).
En
supposant que nous ayons trouvé la solution, se pose alors le problème du
financement. Peut-on, sans risque proposer un prix qui ne dépende pas du
consentement à payer, par exemple un abonnement égal à ![]() ? Tout va bien
si chacun des
? Tout va bien
si chacun des ![]() est plus grand que
est plus grand que ![]() . En revanche si (et c’est évidemment le plus souvent le
cas), certains
. En revanche si (et c’est évidemment le plus souvent le
cas), certains ![]() sont inférieurs à
sont inférieurs à ![]() , ces consommateurs ne s’abonnent pas et l’ouvrage ne pourra
pas être financé. Ce phénomène est ce que l’on appelle un phénomène
d’ “ anti-sélection ” ou d’ “ écrémage ” involontaire
qui est l’un des problèmes centraux liés aux biens publics. Quelles sont dans
ces conditions les portes de sortie ?
, ces consommateurs ne s’abonnent pas et l’ouvrage ne pourra
pas être financé. Ce phénomène est ce que l’on appelle un phénomène
d’ “ anti-sélection ” ou d’ “ écrémage ” involontaire
qui est l’un des problèmes centraux liés aux biens publics. Quelles sont dans
ces conditions les portes de sortie ?
“ La
solution repose sur le principe général suivant : c’est qu’il faut
demander pour prix non ce qu’il coûte mais une somme en rapport avec
l’importance qu’attache celui auquel il est vendu ”, Jules DUPUIT. Certes,
mais comment faire pour y parvenir, chacun n’aura-t-il pas la tentation de
dissimuler le prix qu’il est prêt à payer ? Et si par hasard on peut
estimer indirectement ce prix, la discrimination qui en résulte est-elle
légitime ?
3. Définitions
La
façon la plus simple de définir un “ bien public ” ou
“ collectif ” se fait par opposition au bien privé. Lorsque je
consomme un plat de cassoulet, ou lorsque j’utilise mon magnétoscope, ce
cassoulet précisément, c’est-à-dire physiquement, ne peut être consommé par
personne d’autre puisque c’est moi qui le mange. De même ce magnétoscope que
j’utilise en ce moment ne peut pas être utilisé par quelqu’un d’autre que moi à
ce même moment. Ce sont là des biens
privés au sens où il y a rivalité dans la consommation.
Dès que je consomme (ou utilise) une certains quantité de bien, j’empêche physiquement mon voisin de consommer ce que je consomme. Ce phénomène de rivalité est au centre de l’économie ; c’est parce qu’il y a rivalité et rareté que se pose le problème de la répartition des ressources entre les différents membres d’une société.
Formellement, si on note xi la
quantité d’un certain bien privé consommée par l’individu i,
la quantité totale x qui doit être disponible pour satisfaire la
consommation de n individus doit, par la force des choses être égale à
![]()
Un
bien public, au contraire, ne suppose aucune rivalité dans la consommation. Si
ce bien public est produit en quantité x, tous les consommateurs
peuvent consommer chacun l’intégralité du bien public.
Définition
1: Bien Public Pur.
On dit que [y]
est un bien public pur si, yi étant la quantité de
bien consommée par l’individu i,
la quantité totale qui doit être disponible pour satisfaire la consommation des
n individus est égale à: y = max(yi ).
A
cette condition de non rivalité, on ajoute parfois, pour définir un bien
public, une condition de non exclusion, ou de manière plus forte, une
condition d’obligation d’usage. On dit qu’un bien est sans exclusion
lorsqu’on ne peut pas empêcher un consommateur de consommer le bien (par
exemple en le faisant payer une redevance dissuasive). On dit qu’il y a obligation
d’usage lorsque aucun consommateur ne peut choisir de ne pas consommer le bien.
Ces deux caractéristiques sont liées à des considérations institutionnelles ou
technologiques qui peuvent contraindre les mécanismes de financement. Ici, nous
ne retiendrons que la définition technique d’un bien public pur : la
condition de non rivalité.
Il
existe en fait un grand nombre de cas intermédiaires entre bien privé et bien
public pur. C’est le cas des biens pour lesquels la rivalité est partielle au
sens où lorsqu’un individu consomme un peu plus de bien, il gêne les autres
consommateurs. Ce type de bien, dont l’exemple le plus évident est celui des
biens publics soumis à “ encombrement ”.
4.
Equation de BOWEN-LINDAHL-SAMUELSON, premier
rang.
La
première question qui se pose est une question normative : faut-il
“ construire ” le bien public et à quel niveau ? Supposons pour
simplifier qu’il existe 2 biens dans l’économie, 1 bien public [y]
et un bien privé [x] pris comme numéraire. On
suppose que chaque individu arbitre entre les deux biens au moyen d’une
fonction d’utilité ui. Ainsi ui(yi, xi)
représente l’utilité du consommateur i lorsqu’il consomme xi
unité du bien privé, et yi unités du bien public. On suppose que la
production d’une quantité y de
bien public engendre un coût C(y) en numéraire. Les ressources initiales de
l’économie se résument à W
unités de bien privé réparties entre les consommateurs : W
= ![]() . On suppose enfin que les fonctions d’utilité sont
croissantes en fonction de leur deux arguments. Dans ces conditions,
l’optimalité, ou plutôt l’efficacité requiert yi = y.
Il serait en effet absurde, du point de vue de l’efficacité de ne pas faire
profiter chaque consommateur de l’intégralité du bien public.
. On suppose enfin que les fonctions d’utilité sont
croissantes en fonction de leur deux arguments. Dans ces conditions,
l’optimalité, ou plutôt l’efficacité requiert yi = y.
Il serait en effet absurde, du point de vue de l’efficacité de ne pas faire
profiter chaque consommateur de l’intégralité du bien public.
Réalisabilité et rationnalité individuelle
Définition
2
l’allocation
(y, xi) est réalisable et individuellement rationnelle avec y>0
si et seulement si :
![]() (1)
(1)
![]() (2)
(2)
Cette
condition est une condition nécessaire pour qu’une production y
de bien public soit Pareto améliorante, étant données les ressources initiales.
Définissons
alors la quantité Fi(y)
de numéraire vérifiant :
![]() (3)
(3)
Fi
représente exactement le “ consentement brut ” à payer de l’individu i
pour passer de 0 à y. Notons que ce
consentement brut à payer peut être négatif (auquel cas le bien public lèse
l’individu en question[1]).
On a alors le résultat évident suivant :
Propriété
1
:
y
est une quantité de bien public associée à une allocation réalisable et
individuellement rationnelle si et seulement si :
![]() (4)
(4)
On
interprète cette condition en disant que la somme des consentements bruts à
payer y
est plus grande que le coût.
Efficacité
L’inéquation
(4) ne dit pas que y est efficace. Elle dit simplement que produire y
est plus efficace que ne rien produire ! Nous devons alors chercher sous
quelles conditions (nécessaires) y,
est associée à une allocation efficace. Une condition nécessaire pour que y soit
associée à une allocation efficace est qu’il n’existe pas de variante
“ autour de y ” qui la domine au sens de Pareto. Une
variante est caractérisée par une variation Dy
de bien public et des variations Dxi
de l’allocation en bien privé. Elle est réalisable et Pareto améliorante
si :

Définissons
comme tout à l’heure le consentement à payer de l’individu i pour passer
de l’allocation initiale (y, xi) à
une allocation dans laquelle le bien public est produit en quantité y+Dy, notons ![]() ce consentement à payer (éventuellement négatif).
ce consentement à payer (éventuellement négatif).
![]()
Une
condition nécessaire et suffisante pour que (y, xi)
soit efficace est alors que pour toute variante Dy,
![]() . Cette condition signifie simplement, par exemple pour Dy>0, que la
somme des consentements à payer Dy
ne couvre pas le coût incrémental. Sinon il existerait
. Cette condition signifie simplement, par exemple pour Dy>0, que la
somme des consentements à payer Dy
ne couvre pas le coût incrémental. Sinon il existerait ![]() tels que
tels que ![]() , qui donnerait pour i une utilité
, qui donnerait pour i une utilité ![]() .
.
Définition 3
: On appelle
consentement marginal à payer du consommateur i:

on a évidemment :
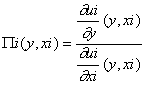
On
a alors le résultat suivant :
Théorème
1: Equation de Bowen-Lindahl-Samuelson
Une condition nécessaire
pour que (y, xi) soit efficace est que :
![]() (5)
(5)
En effet sinon, si ![]() (respectivement
<), on peut trouver Dy>0
(respectivement <0) assez petit en valeur absolue tel que :
(respectivement
<), on peut trouver Dy>0
(respectivement <0) assez petit en valeur absolue tel que :
![]() ,
,
c’est à dire :
![]()
La
condition de Samuelson est la condition de premier rang associée au problème de
bien public. Normativement, c’est l’équation que doit vérifier l’allocation
optimale qui garantit l’efficacité au sens de Pareto.
Il
existe un cas particulier intéressant qui permet de mettre en évidence les problèmes
pratiques associés à la décision publique. Supposons par exemple que ![]() ne dépend pas de xi. Il est facile de voir
qu’alors
ne dépend pas de xi. Il est facile de voir
qu’alors ![]() , le consentement marginal à payer est exactement égal à la
dérivée du consentement brut à payer. Posons alors
, le consentement marginal à payer est exactement égal à la
dérivée du consentement brut à payer. Posons alors ![]() . S s’interprète comme le surplus collectif associé à y.
Les conditions ci-dessus signifient alors que le production efficace doit
maximiser le surplus S, à condition bien sûr que le surplus obtenu soit positif.
Il existe alors un degré de liberté sur la clé de répartition du financement,
on doit avoir
. S s’interprète comme le surplus collectif associé à y.
Les conditions ci-dessus signifient alors que le production efficace doit
maximiser le surplus S, à condition bien sûr que le surplus obtenu soit positif.
Il existe alors un degré de liberté sur la clé de répartition du financement,
on doit avoir ![]() et
et ![]() . Tout se passe alors comme si la décision publique se
décomposait en deux étapes successives. La première consiste à trouver y qui
maximise le surplus, c’est à dire tel que la différence entre somme des
avantages individuels et coût soit maximale. La seconde étape consiste à
déterminer la clé de financement, c’est à dire, de façon équivalente à fixer la redistribution du surplus entre les différents individus.
. Tout se passe alors comme si la décision publique se
décomposait en deux étapes successives. La première consiste à trouver y qui
maximise le surplus, c’est à dire tel que la différence entre somme des
avantages individuels et coût soit maximale. La seconde étape consiste à
déterminer la clé de financement, c’est à dire, de façon équivalente à fixer la redistribution du surplus entre les différents individus.
Calcul économique
Tout
projet public fait l’objet en général d’une étude économique préliminaire
visant à en déterminer la rentabilité collective. Théoriquement, c’est la
démarche esquissée ci-dessus qui devrait être mise en oeuvre : parmi toutes les
variantes, choisir celle qui maximise le surplus, vérifier ensuite que ce
surplus est positif, réaliser enfin les transferts nécessaires de manière à
garantir qu’aucun agent n’est lésé dans l’affaire.
Dans
la pratique il est rare que l’intégralité de la démarche ci-dessus soit
effectuée dans toute sa rigueur. Deux erreurs méthodologiques méritent d’être
soulignées.
·La
seule prise en compte du surplus
Dans
de nombreux cas, on se borne à vérifier que le surplus associé à une décision
est positif pour l’imposer.
On
vérifie alors seulement l’inéquation ![]() .
.
Cette
condition n’est évidemment pas suffisante pour affirmer que le projet est
efficace. On peut être extrêmement loin de la maximisation du surplus. Rien ne
garantit qu’il n’existe pas d’autres variantes qui améliorent significativement
le bilan entre avantages et coût. La démarche rigoureuse consiste à étudier un
ensemble de variantes pour vérifier que le surplus ne peut être amélioré. Ceci
conduit à appliquer la condition de BLS marginale, soit en supposant qu’il n’y
a pas d’effet revenu (![]() ), choisir y tel que:
), choisir y tel que:
![]()
·L’omission
des effets redistributifs.
S’en
tenir au seul arbitrage collectif masque les effets redistributifs de la
décision publique. Ne pas se soucier des transferts qui matérialisent la clé de
répartition du coût peut conduire à une redistribution du surplus inégalitaire et même à des rentes indues.
Imposer un projet public sous prétexte du seul intérêt collectif, sans prise en
compte des surplus individuels, favorise les individus ayant un fort
consentement à payer au détriment de ceux qui ont un consentement petit ou même
négatif.
considérons
par exemple un projet public qui vérifie l’équation de BLS. Supposons de plus
que ![]() et qu’il y ait une
forte hétérogénéité des consentements à payer dans la population : certains ont
un consentement négatif (le projet public les lèse). D’autres ont un
consentement très élevé (le projet les avantage). Pour que le projet soit
efficace et individuellement rationnel il faut mettre en place des transferts
tels que :
et qu’il y ait une
forte hétérogénéité des consentements à payer dans la population : certains ont
un consentement négatif (le projet public les lèse). D’autres ont un
consentement très élevé (le projet les avantage). Pour que le projet soit
efficace et individuellement rationnel il faut mettre en place des transferts
tels que : ![]() , c’est à dire en particulier indemniser les consommateurs
lésés. Cette indemnisation est un coût collectif supplémentaire qui ne peut
être financé que par les consommateurs avantagés. Si l’on indemnise pas les
consommateurs lésés on crée de fait un surplus positif indu (une rente) pour
ceux ayant un consentement à payer positif.
, c’est à dire en particulier indemniser les consommateurs
lésés. Cette indemnisation est un coût collectif supplémentaire qui ne peut
être financé que par les consommateurs avantagés. Si l’on indemnise pas les
consommateurs lésés on crée de fait un surplus positif indu (une rente) pour
ceux ayant un consentement à payer positif.
5.
Décentralisation
Equilibre de marché
Dans
ce qui précède on suppose implicitement qu’une autorité collective est capable
de mener à bien les calculs menant aux conditions d’efficacité.
La
question légitime que l’on peut se poser est de savoir si le marché, c’est à
dire une organisation institutionnelle complètement décentralisée, permet
d’obtenir une allocation efficace. Le plus simple pour y répondre est de
raisonner par conditions nécessaires.
Si
l’on veut que le marché aboutisse à une allocation efficace, il faut que le
prix d’équilibre associé au bien public soit tel que chaque consommateur
demande la quantité de bien public efficace. Ceci imposerait que l’on ait, en
appelant p le
prix du bien public:

L’équation
précédente est la condition nécessaire du premier ordre pour que ![]() maximise
maximise ![]() sous contrainte de
budget
sous contrainte de
budget ![]() . Ceci qui impose en particulier l’égalité des taux marginaux
de substitution (c’est à dire des consentement marginaux à payer), de tous les
consommateurs. Or l’équation de Samuelson n’implique absolument pas l’égalité
(sauf exception) des taux marginaux. Cette première remarque nous conduit alors
à reconsidérer le problème. Un signal prix unique ne suffit pas : il faut
introduire autant de prix qu’il y a de consommateurs. Face à un prix
individualisé pi
le consommateur i émettra une demande telle que l’on ait
:
. Ceci qui impose en particulier l’égalité des taux marginaux
de substitution (c’est à dire des consentement marginaux à payer), de tous les
consommateurs. Or l’équation de Samuelson n’implique absolument pas l’égalité
(sauf exception) des taux marginaux. Cette première remarque nous conduit alors
à reconsidérer le problème. Un signal prix unique ne suffit pas : il faut
introduire autant de prix qu’il y a de consommateurs. Face à un prix
individualisé pi
le consommateur i émettra une demande telle que l’on ait
:
 .
.
Pour garantir l’efficacité il faudrait avoir
:
![]()
Ce
qui est la condition du premier ordre associée à la maximisation du profit de
l’offreur:
![]()
Pour
pouvoir obtenir une allocation efficace comme résultat d’équilibre concurrentiel,
il faut ainsi créer autant de “ marchés ” que de consommateurs : le
commissaire priseur doit ajuster les différents prix individu par individu.
On
voit ainsi que pour obtenir une allocation efficace comme résultat d’un
équilibre de concurrence, on est conduit à créer autant de marchés que
d’usagers. Cette condition est difficilement compatible avec l’hypothèse de
comportement de preneur de prix des consommateurs : chaque usager est seul
demandeur sur son marché, il peut plus facilement mettre à profit cette
situation de monopsone pour tenter de manipuler le prix à son avantage.
Il
existe cependant un cas d’application dans lequel, formellement, le marché est
organisé sur la base de prix personnalisés : il s’agit de la modulation horaire
des tarifs de services tels que le téléphone ou l’électricité. La fourniture de
ce type de service permettant une consommation ![]() à chaque instant,
implique la mise en place d’équipements qui doivent être dimensionnés à un
niveau K
de manière à satisfaire les pointes de demande :
à chaque instant,
implique la mise en place d’équipements qui doivent être dimensionnés à un
niveau K
de manière à satisfaire les pointes de demande : ![]() . Une fois cette capacité mise en place, toute demande
inférieure peut être satisfaite pour un coût égal au seul coût marginal de
court terme (par exemple le coût du combustible); en revanche pour satisfaire
une demande supérieure à la capacité il faut élargir la capacité de production
et donc engager un coût marginal de développement
. Une fois cette capacité mise en place, toute demande
inférieure peut être satisfaite pour un coût égal au seul coût marginal de
court terme (par exemple le coût du combustible); en revanche pour satisfaire
une demande supérieure à la capacité il faut élargir la capacité de production
et donc engager un coût marginal de développement ![]() . Formellement, la capacité est un bien public au sens où
elle est entièrement disponible à des instants différents : son utilisation à
un instant donné n’empêche absolument pas son utilisation à un autre moment.
C’est une caractéristique de non rivalité temporelle formellement équivalente à
la condition de non rivalité des biens publics traditionnels. Dans ces
conditions, les prix personnalisés s’interprètent comme les prix d’usage à
chaque instant. La condition de BLS signifie alors que la somme des prix
instantanés (c’est à dire le prix associé à l’usage permanent de
l’infrastructure) doit être égal au coût marginal de développement.
. Formellement, la capacité est un bien public au sens où
elle est entièrement disponible à des instants différents : son utilisation à
un instant donné n’empêche absolument pas son utilisation à un autre moment.
C’est une caractéristique de non rivalité temporelle formellement équivalente à
la condition de non rivalité des biens publics traditionnels. Dans ces
conditions, les prix personnalisés s’interprètent comme les prix d’usage à
chaque instant. La condition de BLS signifie alors que la somme des prix
instantanés (c’est à dire le prix associé à l’usage permanent de
l’infrastructure) doit être égal au coût marginal de développement.
Négociation en information complète
Une
autre possibilité, en l’absence de centre calculateur, consiste à supposer que
les différents consommateurs sont capables de négocier librement pour aboutir à
un consensus. Lorsque l’information est complète, c’est à dire lorsque chaque
agent connaît les préférences des autres, on peut montrer que le processus de
négociation est efficace.
Supposons
par exemple le modèle simple sans effet revenu (![]() ). A chaque décision y est associée un surplus
collectif
). A chaque décision y est associée un surplus
collectif ![]() . Si les transferts entre les agents sont possibles, une
allocation est caractérisée par une répartition du surplus, chaque consommateur
se retrouvant finalement avec un surplus individuel
. Si les transferts entre les agents sont possibles, une
allocation est caractérisée par une répartition du surplus, chaque consommateur
se retrouvant finalement avec un surplus individuel ![]() positif vérifiant
positif vérifiant ![]() . Le processus de négociation prend la forme de propositions
et de contre-propositions sur y et la répartition
. Le processus de négociation prend la forme de propositions
et de contre-propositions sur y et la répartition ![]() . Sans rentrer dans le détail du jeu de négociation, on peut
cependant donner l’intuition du résultat.
. Sans rentrer dans le détail du jeu de négociation, on peut
cependant donner l’intuition du résultat.
Il
est d’abord clair qu’une proposition dans laquelle y=y0 est
inefficace n’a aucune chance d’être adoptée par les négociateurs : il est
facile de trouver une contre-proposition dans laquelle y=y1 est
un niveau de bien public donnant un surplus collectif plus grand et une
répartition de ce surplus unanimement préférée par tous les
protagonistes.
La
négociation ne peut donc aboutir qu’à un niveau de bien public efficace. La
répartition du surplus dépend alors de pouvoir relatif de négociation de chacun
des protagonistes.
Ce
résultat d’efficacité de la négociation repose crucialement sur l’hypothèse
d’information complète : lorsqu’un négociateur fait une proposition il sait à
l’avance qu’elle sera acceptée ou refusée par tel ou tel autre agent. Ainsi la
négociation s’arrête lorsqu’un état efficace est atteint, elle se poursuit si
l’on peut trouver une allocation qui améliore le bien-être de chacun.

Second rang
Lorsque
“ la puissance publique ” est parfaitement informée, la décision de
mise en place et celle du financement du bien public peuvent être menées
indépendamment : d’abord trouver y qui maximise le surplus,
ensuite fixer les contributions individuelles ti , ![]() , de sorte que
, de sorte que ![]() .
.
Tout
change bien sûr lorsque l’Etat ne possède qu’une information imparfaite sur les
consentements à payer individuels.
Supposons
d’abord que l’Etat est en mesure de connaître uniquement la somme des
consentements à payer ![]() sans pouvoir observer
le consentement individuel de chacun.
sans pouvoir observer
le consentement individuel de chacun.
L’Etat
peut calculer le niveau optimal de bien public en résolvant l’équation de BLS.
En revanche il se heurte à un problème informationnel lorsqu’il doit fixer les
contributions individuelles. S’il fixe
une contribution uniforme égale à ![]() , rien ne garantit que chaque consommateur aura augmenté son
bien-être par rapport au status-quo. C’est le cas en particulier lorsque
, rien ne garantit que chaque consommateur aura augmenté son
bien-être par rapport au status-quo. C’est le cas en particulier lorsque ![]() . Dans ce cas l’allocation finale n’est pas plus efficace que
le status quo : certains voient leur bien-être diminuer.
. Dans ce cas l’allocation finale n’est pas plus efficace que
le status quo : certains voient leur bien-être diminuer.
On
pourrait imaginer que l’Etat mette en place un mécanisme qui s’apparente à un
mécanisme d’enchère : chacun doit annoncer son consentement à payer. Si la
somme n’est pas celle prévue alors le bien public n’est pas réalisé. Si la
somme est celle prévue alors on réalise le bien et on demande à chacun une
contribution telle que le surplus individuel net ![]() soit constant égal à
soit constant égal à ![]() . Annoncer son véritable consentement à payer est une
stratégie d’équilibre de Nash : si les autres annoncent la vérité alors chaque
individu a intérêt à annoncer la vérité. Evidemment, dès qu’il y a incertitude
sur la somme des consentements, le résultat ne tient plus.
. Annoncer son véritable consentement à payer est une
stratégie d’équilibre de Nash : si les autres annoncent la vérité alors chaque
individu a intérêt à annoncer la vérité. Evidemment, dès qu’il y a incertitude
sur la somme des consentements, le résultat ne tient plus.
Tout
se complique lorsque l’autorité collective n’a pas d’information a priori ni
sur la somme des consentements à payer ni sur leur valeur individuelle. La
section complémentaire à ce chapitre présente un mécanisme de révélation qui
permet de s’affranchir en partie de ce problème.
D’une
manière générale, lorsque l’absence d’information interdit l’usage de
transferts individuels forfaitaires, le financement du bien public ne peut se
faire qu’à l’aide d’instruments indirects. On peut concevoir différentes
options : le financement fondé sur l’usage en introduisant une charge d’accès
ou un péage, le financement fondé sur des ressources fiscales prélevées sur la
consommation ou la production d’autres biens.
L’introduction
d’un péage, lorsqu’il est possible techniquement, c’est à dire lorsque le bien
public peut faire l’objet d’exclusion, soulève le problème général
d’antisélection ou d’écrémage involontaire. La section
complémentaire propose un modèle simple qui permet d’expliquer le phénomène.Le
financement par la fiscalité implique des distorsions dans les prix des autres
biens. Ces distorsions introduisent elle-mêmes des inefficacités puisque les
prix ne sont plus les prix d’équilibre
concurrentiel. Nous reviendrons plus loin, dans le chapitre consacré à la
fiscalité; sur ce type de problème.
Section complémentaire :
mécanismes de Vickrey, souscription…